Il mondo matematico, le logiche ad esso sottese, la sua razionalità intrinseca sembrano apparentemente distanti anni luce dalla bellezza artistica e dalle sue svariate forme espressive.
Può risultare lecito chiedersi se la volontà di razionalizzare l’arte, cercarne un canone oggettivo possa in realtà annientare la creatività. Il rapporto tra arte e matematica, però, esiste eccome, e la convergenza tra questi due mondi è sempre stata in qualche modo presente, sin dall’antichità.
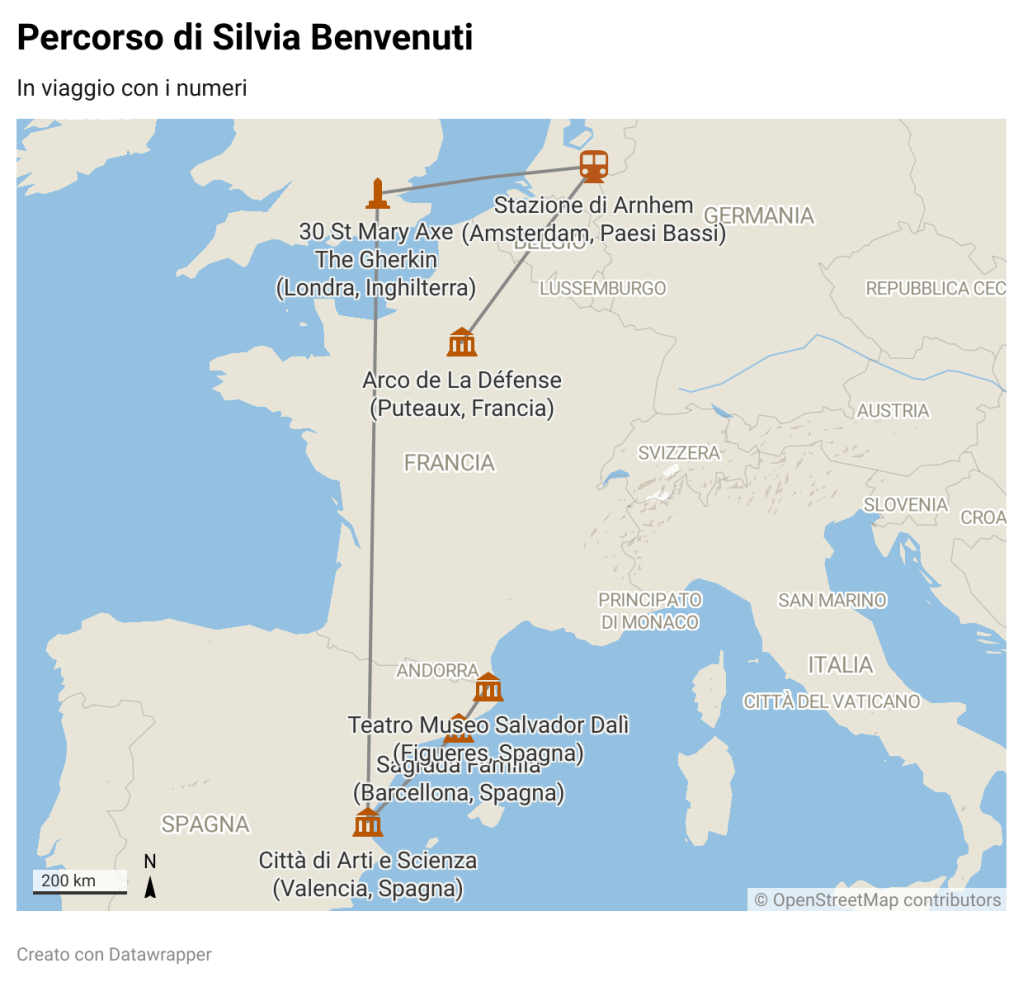
Il Podcast di Rai Radio 3 diretto da Anna Maria Giordano, Lovely Planet, ci ha regalato una puntata estremamente curiosa in merito, che si propone di mostrarci sotto una nuova lente (matematica) alcune delle più famose opere d’arte europee, dalla Spagna all’Olanda, alla Francia. Ad accompagnarci in questo viaggio ― una passeggiata per mateturiste/i curiose/i ― Silvia Benvenuti: matematica, autrice, divulgatrice e ospite con il suo intervento.
Partiamo dal nord-est della Spagna, nei pressi di Figueres: vivace città dell’entroterra catalano, conosciuta specialmente per essere la sede del Teatro-Museo Salvador Dalì, e per aver dato i natali al noto pittore surrealista.
Quando pensiamo al Surrealismo, alla sua peculiare dimensione onirica e irrazionale, difficilmente immaginiamo possa esserci un legame con delle regole rigidamente logiche. E invece Dalì, uno dei maggiori esponenti di questa corrente, era un grande amante e studioso della matematica. Nel suo libro 50 segreti dell’artigianato magico, l’artista spiega chiaramente il ruolo che tale disciplina e i suoi principi hanno nella realizzazione dei propri quadri: «Giovane pittore, sì, sì, sì e sì! Devi, soprattutto da giovane, usare la geometria come guida alla simmetria nella composizione delle tue opere. So che i pittori più o meno romantici sostengono che queste impalcature matematiche uccidono l’ispirazione dell’artista, dandogli troppo su cui pensare e riflettere. Non esitare un attimo a rispondere loro prontamente che, al contrario, è proprio per non avere da pensare e riflettere su queste cose, che tu le usi». E così, anche nei suoi lavori che ci sembrano più “irrazionali”, la ratio, invece, è ovunque; così come è sempre riscontrabile, per un occhio più attento, la fascinazione di Dalì per le teorie matematiche.

Prendiamo in considerazione Corpus Hypercubus, quadro che raffigura una Crocifissione decisamente inusuale. Cristo non è sorretto dalla solita croce, ma sembra fluttuare magicamente in uno spazio tridimensionale in cui Dalì vuole rappresentare il cosiddetto ipercubo, la generalizzazione del cubo oltre la terza dimensione. Non erano infatti sfuggiti a Dalì gli studi sulla quarta dimensione, assai affascinanti e perfettamente compatibili con il suo intento di rappresentare una realtà trascendentale, al di là dello spazio e del tempo. Oltre alle tre dimensioni a noi ben note (lunghezza, altezza e profondità), va infatti aggiunta una quarta, il tempo, che consente di generalizzare concetti geometrici elementari e dare loro una nuova vita. È il dispiegamento di un cubo su un piano, che crea una figura somigliante a una croce, a ispirare la rappresentazione metafisica di Cristo, carica di simbolismo, che non possiamo realmente “vedere”, ma soltanto percepire.
Dalì prende spunto da svariati temi della teoria matematica a lui contemporanea. Nel Novecento questa, come d’altronde ogni altra disciplina, attraversa un periodo di straordinario sviluppo e viene persino paragonata dal matematico tedesco Hermann Weyl al Delta del Nilo, le cui acque si estendono in ogni direzione.
Non c’è dubbio, infatti, che verso gli anni Cinquanta Dalì sia rimasto affascinato dalla Teoria delle catastrofi sviluppata da René Thom, tanto da dedicarvi una serie di quadri, fra cui Coda di rondine e violoncelli e Ratto topologico d’Europa, ispirati alle cosiddette catastrofi naturali. Tali studi, a differenza di quanto suggerisce il nome, non hanno nulla di catastrofico: senza entrare troppo nel tecnico, questi trattano della morfogenesi di particolari figure, e una catastrofe è semplicemente un punto critico, nel quale una curva cambia natura. La Teoria delle catastrofi, in realtà, non è altro che un tentativo di applicazione della topologia, una branca della matematica che deforma le figure senza effettuare “strappi, sovrapposizioni o incollature” e tratta gli oggetti matematici come se questi fossero fatti di plastilina. I famosissimi “orologi molli” di Dalì, di cui troviamo rappresentazione emblematica nel quadro La persistenza della memoria, non sono altro che oggetti topologici, deformati allo scopo di mostrare l’aspetto psicologico del tempo. Lo stesso Teatro-Museo Dalì costituisce un esempio lampante della fascinazione del pittore per le intriganti teorie matematiche, nonché un’occasione per vivere a 360 gradi il suo mondo surrealista.


Sempre in Spagna, questa volta a Barcellona, sarebbe impensabile non soffermare la nostra attenzione sulle opere architettoniche di Antoni Gaudì, in particolare la Sagrada Familia, simbolo indiscusso della città. Personalità estremamente eccentrica, religioso fervente e studente decisamente irregolare, al conferimento del diploma di laurea, il direttore della facoltà dichiarò: «Non so se abbiamo conferito il titolo a un pazzo o a un genio, con il tempo si vedrà». Ed effettivamente il tempo ha dato le sue risposte: Gaudì è al giorno d’oggi considerato uno dei massimi esponenti del modernismo e le sue opere a Barcellona figurano dal 1984 nella lista del patrimonio dell’umanità dell’Unesco. La chiave artistica dell’architetto è la superficie curva, alla quale conferisce un profondo significato religioso, secondo la convinzione che «la linea retta appartiene all’uomo, mentre la curva è la linea di Dio». Gaudì fonda il suo particolare stile proprio con l’intento di rendere gloria a Dio e, benché a un primo impatto le sue costruzioni possano apparire assemblate senza alcun rigore o coerenza, in realtà ognuna di esse trasuda formalizzazioni matematiche e geometriche evidenti, se solo ci si sofferma più attentamente. Sperimenta molto con le superfici rigate (che in geometria, per semplificare, non sono altro che superfici composte da molte linee, la cui unione forma la superficie stessa), ma non si accontenta delle più comuni, quali il piano, il cilindro e il cono.

La prima superficie rigata a suscitare forte interesse nell’architetto spagnolo è senza dubbio l’iperboloide iperbolico, che non è altro che un cilindro le cui basi sono state ruotate in sensi opposti in modo da ottenere una sorta di clessidra. Ritroviamo sistematicamente questa struttura per la progettazione delle colonne nelle sue costruzioni e, anche in questo caso, non si tratta certamente di una scelta solo stilistica. Non era infatti sfuggito a Gaudì che il femore, fondamentale per reggere il peso del nostro corpo, ricorda proprio un iperboloide, e se Dio avesse ritenuto più adatto un cilindro, per realizzare tale compito, allora il nostro femore non avrebbe certo questa forma.
Ma è un’altra la rigata che conquista veramente Gaudì: si tratta della cosiddetta superficie a forma di sella, o, formalmente parlando, il paraboloide iperbolico. Questa superficie è descritta da una retta che scorre parallelamente a sé, la generatrice, e che si muove su due rette sghembe. Che siate riuscite/i a visualizzarla o meno, basti sapere che in essa Gaudì ritrova la perfetta rappresentazione della Trinità, dal momento che «una retta infinita rappresenta il Padre, l’altra il Figlio, la terza lo Spirito Santo, che relaziona amorosamente gli altri due».


Lasciamo ora le strade di Barcellona, ma non la Spagna, e continuiamo a percorrere la costa verso sud, fino a Valencia, la Città delle Arti e delle Scienze. Qui, architettura classica e moderna si incontrano grazie al particolare contributo dell’architetto Santiago Calatrava che, per rendere omaggio alla città natale, ne ha riempito gli spazi con grandi linee curve e leggere, caratteristica peculiare di ogni sua opera: dall’emblematico Museo delle scienze, all’edificio monumentale Agorà; dal Ponte di Calatrava (Assut de l’Or) alla Terrazza espositiva Umbracle.

La matematica acquisisce così un’essenza tutta nuova: non è solo supporto strumentale, ma un vero e proprio supporto creativo, e quest’idea diventa presto una tendenza che ispira e intriga artisti e artiste di tutta l’Europa. Ad esagerare il concetto, ci pensa la coppia di architetti olandesi Ben Van Berkel e Caroline Bos, che nei loro progetti si ispirano a forme matematiche che non siamo nemmeno in grado di visualizzare. La casa di Möbius, per esempio, fa riferimento alla Striscia di Möbius, una superficie non orientabile composta da due linee continue che si intersecano a formare una doppia spirale. Nella costruzione, gli spazi sono stati progettati secondo questa logica: la traiettoria incrociata dell’anello si riferisce al ciclo di vita e di lavoro di una famiglia lungo le 24 ore della giornata; quando l’anello si inverte, l’involucro esterno in cemento si trasforma in mobili interni e le facciate in vetro diventano partizioni interne. I materiali si incrociano e si scambiano, i pavimenti diventano soffitti, le finiture esterne diventano mobili. Un altro esempio dei due architetti, fra gli svariati che si potrebbero fare, è la Stazione di Arnhem Centrale, che prende spunto dal continuo scambio di superficie interna ed esterna della bottiglia di Klein. Quest’ultima è una particolare figura geometrica non orientabile, nella quale cioè non si può individuare un sopra e un sotto, un esterno e un interno.


Lasciamo ora la seducente architettura olandese di Van Berkel e Caroline Bos e spostiamoci in Francia, per concludere questo percorso fra arte e matematica. Anche le Grande Arche de la Fraternité di Parigi, noto più semplicemente come il Grande Arco, in realtà non è altro che una rappresentazione quasi perfetta dell’ipercubo svuotato al suo interno, realizzato a seguito di un concorso internazionale indetto nel 1982 e considerato uno degli edifici più moderni e iconici della capitale francese.
Per concludere, Silvia Benvenuti ci ricorda che, per poter apprezzare veramente l’arte, dobbiamo sforzarci di eliminare tutti i limiti che condizionano le nostre idee. Per esempio, spesso si tende a riconoscere bellezza e valore solo a ciò che è stato realizzato (paradossalmente) almeno 3000 anni fa, approcciandosi quindi al mondo dell’arte moderna con forti pregiudizi. In realtà, questa nasce proprio dal rifiuto di credere che le possibilità di sviluppo artistico siano ormai “esaurite” nel passato e dalla volontà di continuare a sperimentare creativamente in modi sempre nuovi e mai banali.
La puntata integrale del Podcast Lovely Planet di Rai Radio 3 è disponibile al seguente link: https://www.raiplaysound.it/audio/2022/08/Radio3-Mondo-del-17082022-4feb1b03-4a4a-4da5-94b1-d1dab6370333.html
In copertina: Teatro-Museo Salvador Dalì.
***
Articolo di Chiara Giacomelli

Laureanda in Management presso l’Università di Pavia. Ama le cene in compagnia e leggere un libro che la tenga incollata fino ad addormentarcisi sopra. Ha tanti sogni nel cassetto, ma non sa da quale cominciare… perciò per adesso si limita a “fare la fuorisede” e a scrivere la tesi, sempre in compagnia delle sue cuffiette, da cui non si separa mai, e di una tazza di tè fumante.



Un commento