La cultura della corda è stato un fattore determinante nella migrazione dell’umanità fuori dall’Africa. Se non ci fossero state borse in cui contenere le provviste e corde cui appendere le borracce di uova di struzzo o zucca lagernaria, i gruppi umani difficilmente sarebbero riusciti ad allontanarsi dai loro territori ancestrali.
Collegato alla produzione di corda vi è il gioco della matassa il cui significato dipende dalle persone intervistate. C’è chi dice che rappresenti una trappola e chi pensa che simboleggi l’unità, oppure è visto come una metafora dell’interconnessione dell’universo. Indipendentemente dall’interpretazione data, il gioco delle figure-con-la-corda (Fclc) ha una storia ricca e un messaggio potente.
L’onnipresenza delle Fclc nelle varie culture umane stimola la ricerca del “come mai”? Kaaronen et al. sottolineano due aspetti: il ruolo fondamentale del gioco nello sviluppo umano e la grande disponibilità di corde nelle tradizioni materiali. Non c’è dubbio che il gioco della matassa favorisca la coordinazione occhio-mano e le abilità motorie fini. Giocare a Ripiglino implica l’uso simultaneo di entrambe le mani, in sinergia con lo sguardo, e richiede movimenti articolati delle dita. Questi gesti aiutano bambini e bambine a sviluppare sensibilità tattile, precisione nei movimenti e a rafforzare la muscolatura delle dita, migliorandone la destrezza. Inoltre il gioco stimola la creatività e l’immaginazione, incoraggiando a pensare fuori dagli schemi ed esplorare le proprie capacità artistiche.
L’ubiquità di specifici intrecci potrebbe essere il risultato dei cosiddetti “attrattori” cognitivi teorizzati da Buskell (2017). Secondo questa visione, alcune caratteristiche sia dei fili che dei corpi o delle menti umane creano delle affordance (usabilità) che spiegano la ricorrenza di specifici modelli culturali. Chrisomalis (2020) nel suo Reckonings: Numerals, Cognition, and History sottolinea che i numeri non sono neutri, ma tecnologie cognitive che rendono possibili e/o facilitano (afford) certi tipi di pensiero, calcolo, comunicazione e organizzazione sociale. La “affordance” non è solo la proprietà tecnica o visiva del sistema numerico, ma una qualità che scaturisce dall’incontro tra la forma del sistema numerico (numeri romani o arabi), le capacità cognitive degli utenti e le necessità pratiche e culturali del momento storico.
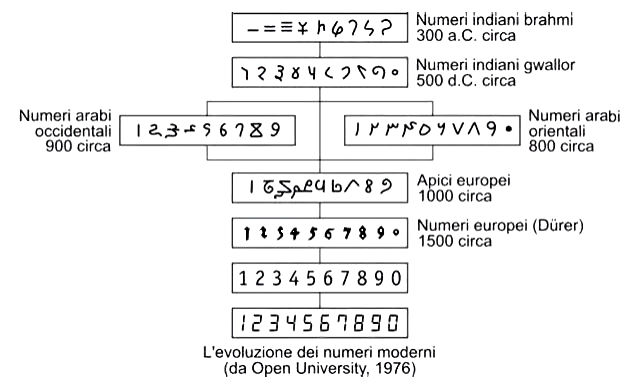
Il sistema numerico Brahmi (India), che risale al III secolo a.C., non conosceva ancora né il concetto di zero né il sistema posizionale che furono sviluppati dai matematici Aryabhata e Brahmagupta nel periodo Gupta (IV-VII sec d.C.). Questi studi diedero vita alle cifre decimali Gwalior. L’invenzione indù fu assimilata dall’Ellenismo giungendo così ai Neo-Pitagorici. Manlio Torquato Severino Boezio (V sec d.C.) ne parla nel suo Ars Geometrica. Le cifre indù, impresse nei gettoni dell’abaco a colonne o gettoni, furono chiamate apici di Boezio o figure d’abaco. Con la conquista della Spagna (711 d.C.) gli arabi appresero le cifre, che chiamarono hindi, riconoscendone l’origine indù. Algoritmo divenne il termine con cui inizialmente era chiamato il sistema di numerazione scritta posizionale nei Paesi latini. Grazie agli algoritmi per rappresentare in forma scritta un numero sono sufficienti i simboli grafici delle unità semplici e dello zero, di numero pari alla base del sistema di numerazione utilizzato.

In sintesi, Chrisomalis usa il concetto di affordance per mostrare che la scelta e l’evoluzione dei sistemi numerici non è solo una questione di efficienza, ma di adattamento culturale e cognitivo alle esigenze di chi li usa. Ad esempio i numeri romani avevano e hanno affordance simboliche e cerimoniali (li vediamo ancora oggi in orologi, monumenti, eventi ufficiali) mentre i numeri arabi (o “occidentali”, come li chiama Chrisomalis) hanno affordance pratiche per il calcolo veloce e la stampa, che ne hanno favorito la diffusione con l’avvento della tipografia. In questo contesto Kaaronen et al. (2023) mettono anche in luce come le nostre capacità corporee, cognitive e percettive condivise abbiano portato all’evoluzione culturale indipendente di unità simili di misurazione e conteggio (Bender and Beller 2012), sistemi numerici simili (Chrisomalis 2020) nonché categorie di costellazioni stellari (Kemp et al. 2022).
Tornando alle Fclc possiamo anche supporre che esse possano essere interpretate come una primitiva forma di pensiero matematico. Storicamente gli studi sull’etnomatematica si sono focalizzati sui sistemi di numerazione o l’uso dei pesi e delle misure, sviluppi che sono relativamente recenti nella storia umana, tuttavia il pensiero matematico oggi non viene più ristretto alla matematica discreta (es. studio delle proporzioni, teoria degli insiemi, calcolo combinatorio ecc.), ma comincia a esplorare anche la cognizione topologica antica.
La topologia è la matematica delle forme e delle deformazioni. Non si interessa a misure precise (come lunghezza o angoli), ma a proprietà invarianti sotto trasformazioni continue — stiramenti, torsioni, piegamenti, tutte operazioni fondamentali nella creazione di Fclc. «La creazione di figure complesse con i fili richiede vari tipi di ragionamento matematico, tra cui il ragionamento algoritmico, la visualizzazione spaziale e il conteggio. Mentre le figure semplici possono essere apprese attraverso l’imitazione, quelle complesse spesso presentano enigmi imprevedibili che richiedono una simulazione mentale esperta di topologia e una profonda comprensione del comportamento dei fili» (Kaaronen et al. 2023). Possiamo dunque porre la pratica di creare Fclc dentro il campo dell’etnomatematica, e più precisamente, in quello dell’etnotopologia (Kaaronen et al. 2023).
Topologia e nodi sono strettamente correlati. La Teoria dei Nodi, che studia i nodi chiusi nello spazio tridimensionale per capire quando due nodi sono “equivalenti”, cioè trasformabili l’uno nell’altro senza tagli né incollaggi, ma solo con deformazioni continue, usa strumenti topologici per classificare e distinguere i nodi. Poiché i nodi “vivono” nello spazio tridimensionale, la loro analisi richiede una comprensione della topologia 3D, come le varietà tridimensionali e le superfici che possono “bordare” un nodo. Aggiungo che la concordanza tra nodi (cioè la possibilità di collegarli tramite una superficie liscia) è un concetto topologico che porta alla definizione di gruppi di concordanza, studiati con tecniche di cobordismo e topologia differenziale. In sintesi la topologia fornisce il linguaggio e gli strumenti per studiare i nodi, mentre la teoria dei nodi esplora come questi oggetti si comportano nello spazio.

Il nome di Leibniz risveglia il mio ricordo liceale della sua teoria filosofica delle “monadi”, nome che nel Veneto permetteva ogni sorta di giochi di parole per l’assonanza con l’epiteto “mona”. Leibniz, in realtà, è stato molto più di una battuta salace tra liceali veneziani. La maggior parte degli studiosi della Teoria dei Nodi propone che essa fondi le sue radici concettuali nella supposizione di Gottfried Wilhelm Leibniz che, accanto al calcolo e alla geometria analitica, dovesse esserci anche una “geometria di posizione” (geometria situs) che trattava le relazioni che dipendevano solo dalla posizione ignorando le grandezze. Nel 1679 egli scriveva a Huygens: «Non mi accontento dell’algebra, in quanto essa non fornisce né le dimostrazioni più concise né le costruzioni geometriche più belle. Di conseguenza, alla luce di ciò, ritengo che abbiamo bisogno di un altro tipo di analisi, geometrica o lineare, che si occupi direttamente della posizione, così come l’algebra si occupa della grandezza». In effetti, in quello stesso anno, nella sua Charateristica Geometrica, Leibniz cercò di formulare alcuni simboli speciali per rappresentare e combinare le figure della geometria situs, dando vita a una prima intuizione dell’odierna topologia combinatoriale. La figura di Leibniz, tra i massimi esponenti del pensiero occidentale, nonché una delle poche figure di “genio universale” in quanto precursore dell’informatica, della neuroinformatica, del calcolo automatico, della dimensione dell’inconscio e della teoria dei nodi, è particolarmente triste.

Egli infatti inventò autonomamente (1684), ma contemporaneamente a Newton (1666 ma pubblicato indirettamente nel 1693), la matematica infinitesimale (ovvero il calcolo differenziale e integrale), ma nella disputa di plagio che seguì, Leibniz, un immigrato tedesco in Inghilterra, perse. La Royal Society, presieduta da Newton stesso, matematico e fisico ufficiale del re, stabilì che la scoperta prioritaria era del fisico inglese. La disputa continuò anche dopo la morte dei due e divenne una querelle tra Inghilterra e Germania (poi l’Europa continentale). Infatti, la forma differenziale di Leibniz fu adottata dai matematici continentali e respinta invece dagli inglesi che, proprio per questa loro posizione di principio, incontrarono non pochi ostacoli nello sviluppo delle ricerche infinitesimali. Oggi viene usata la forma di Leibniz per le notazioni differenziali come funzione y=f(x), ∫= integrale e derivata dy/dx.

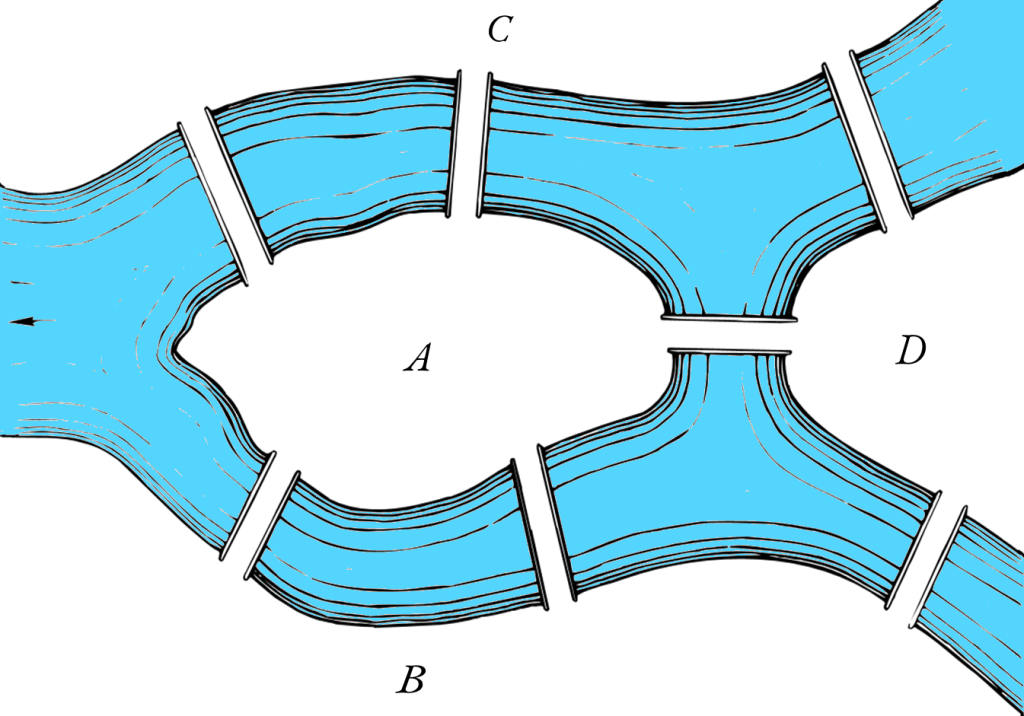
Il primo esempio convincente di geometria situs fu studiato da Leonard Euler (Eulero). Si tratta del “problema dei ponti di Königsberg” (oggi Kaliningrad). La città è attraversata dal fiume Pregel e comprende due isole collegate tra loro e con le rive del fiume da sette ponti. Gli abitanti si chiedevano: «È possibile fare una passeggiata che attraversi ciascun ponte una sola volta e torni al punto di partenza?». Eulero risolse il problema dei ponti. Egli rappresentò le aree di terra come nodi (A, B, C, D) e i ponti divennero archi che collegano i nodi. Analizzò poi il grado di ciascun nodo (cioè il numero di ponti che vi arrivano o partono) dimostrando che un cammino euleriano (che attraversa ogni arco una sola volta) è possibile solo se ci sono al massimo due nodi con grado dispari. Poiché nel caso di Königsberg, tutti e quattro i nodi avevano grado dispari, quindi non esisteva un tale cammino. Nel 1736 Eulero presentò la sua soluzione all’Accademia delle Scienze di San Pietroburgo (fondata da Leibniz), ponendo le basi della teoria dei grafi e della topologia.
In copertina: Out Of Africa, interpretazione della migrazione dall’Asia alle Americhe. Sottolineo la presenza di corda / filo per tenere insieme le pelli, basto a fronte per portare pesi e masserizie, corda per attaccare le punte di lancia o arpione al supporto ligneo, ecc.
***
Articolo di Flavia Busatta

Laurea in Chimica. Tra le fondatrici di Lotta femminista (1971), partecipa alla Second World Conference to Combat Racism and Racial Discrimination (UN Ginevra 1983) e alla International NGO Conference for Action to Combat Racism and Racial Discrimination in the Second UN Decade, (UN Ginevra 1988). Collabora alla mostra Da Montezuma a Massimiliano. Autrice di vari saggi, edita HAKO, Antrocom J.of A.


