Nei precedenti articoli abbiamo visto come le praticanti trobriandesi mostrano generalmente la figura-con-la-corda (Fclc) al pubblico per pochi istanti, prima di disfarla in modo sistematico tramite una lunga procedura necessaria per sciogliere l’intreccio complesso, che generalmente un principiante trasforma in un nodo inestricabile. «Questa osservazione sembra confermare che la figura ottenuta è percepita solo come una fase di un processo che riporta all’anello di filo iniziale. Ciò suggerisce ancora una volta che le praticanti trobriandesi attribuiscono un’importanza fondamentale alla procedura nel suo complesso. L’aspetto procedurale dei giochi con la corda è evidenziato anche dal ritmo che le praticanti imprimono alla realizzazione di una figura con la corda. Le procedure del gioco con la corda sono infatti scandite da un’esecuzione cadenzata delle operazioni. L’esempio della procedura magiaweda (pipistrello) mostra molto chiaramente che alcuni gesti sono accentuati dalla praticante, a volte in modo quasi esagerato, nel senso che tale accentuazione non è tecnicamente necessaria. In particolare, le operazioni di inserimento di un dito in un anello sono molto amplificate. Inoltre, tra ciascuna delle operazioni è prevista una breve pausa, che ha l’effetto di sequenziare la procedura agli occhi dell’osservatore». (Vandendriessche 2015).

Il Ripiglino può dunque essere considerato una attività matematica, ovvero una “procedura” (o un “algoritmo”) composta da una successione di operazioni elementari che possono essere equiparate a procedure, sottoprocedure, processi iterativi, ecc…
Abbiamo visto come molte menti geniali da Leonardo a Durer, a Leibniz a Eulero fossero interessate ai nodi, a cercare di formulare la disciplina che diventerà la topologia. Tuttavia dopo la brillante soluzione di Eulero dell’enigma dei ponti di Könisberg, si dovette attendere fino al 1771 prima che Alexandre-Theophile Vandermonde formulasse le Remarques sur les problèmes de situation.
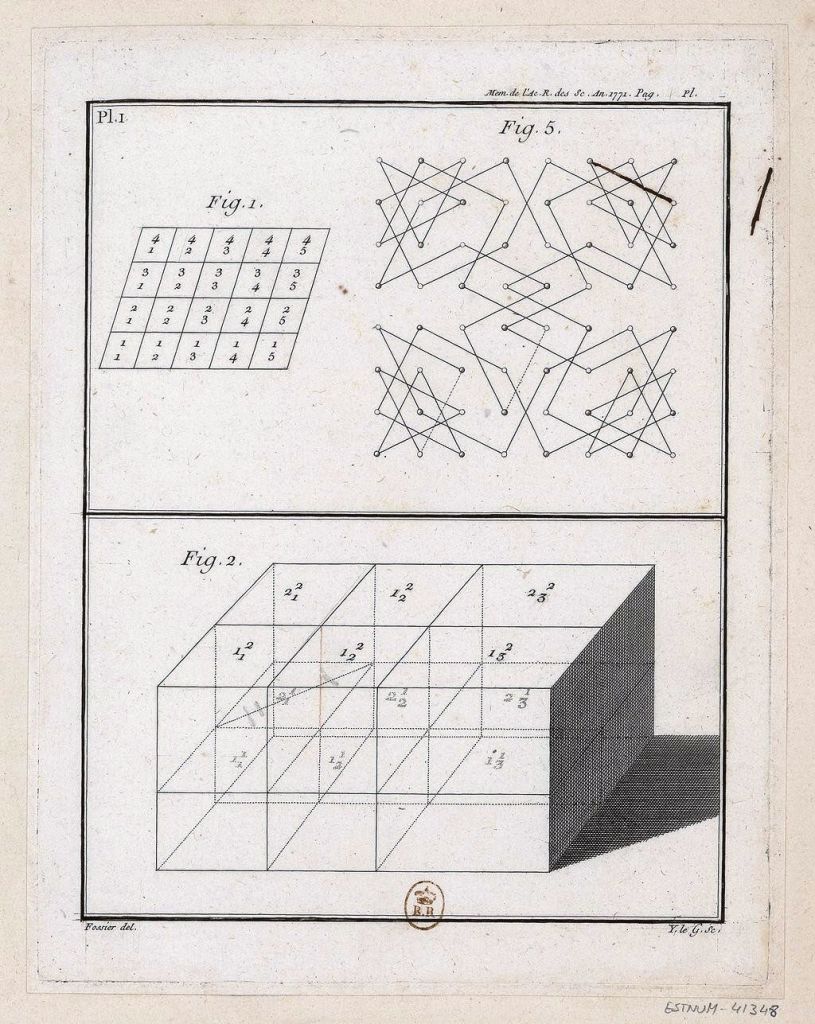
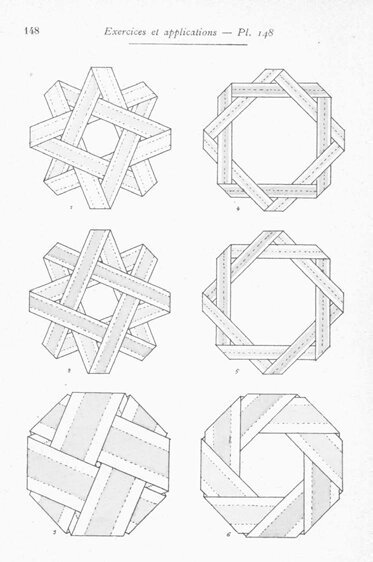
Egli infatti scriveva: «Qualunque siano le curve e le svolte di un sistema di fili nello spazio, è sempre possibile ottenere un’espressione per il calcolo delle sue dimensioni, ma tale espressione sarà di scarsa utilità nella pratica. L’artigiano che realizza una treccia, una rete o dei nodi non si preoccuperà delle questioni relative alla misurazione, ma piuttosto di quelle relative alla posizione: ciò che vede è il modo in cui i fili sono intrecciati».
Non dimentichiamo che il XVIII secolo è quello della rivoluzione industriale e dei telai meccanici.

L’alba della Teoria dei Nodi apparve con Carl Friedrich Gauss. Nella sua nota (22 gennaio 1833) Gauss introdusse attraverso un metodo analitico il numero di collegamento di due nodi (linking number). L’integrale di Gauss nella teoria dei nodi collega analisi matematica e topologia, in particolare attraverso l’invariante noto come numero di collegamento di Gauss (linking number o Gln). L’integrale di Gauss è usato per calcolare il numero di collegamento tra due curve chiuse nello spazio tridimensionale ovvero quante volte una curva “avvolge” l’altra, ed è uno dei primi invarianti topologici studiati nella teoria dei nodi.
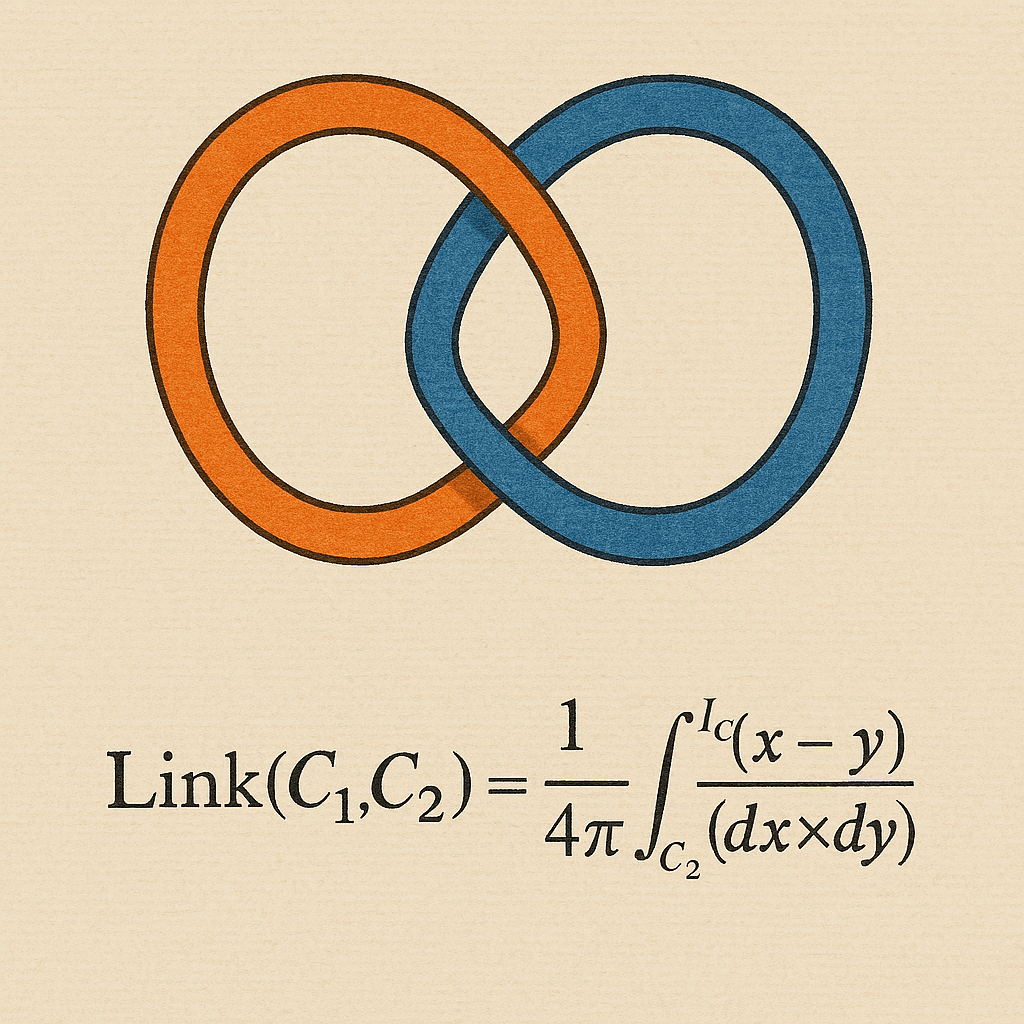
Immaginate due anelli chiusi immersi nello spazio tridimensionale, che si incrociano esattamente una sola volta. Questa configurazione prende il nome di intreccio di Hopf (Hopf link), in onore del matematico tedesco Heinz Hopf. Si tratta di un “nodo” composto da due cerchi che, pur non toccandosi fisicamente, risultano inseparabili senza tagliare almeno uno dei due.

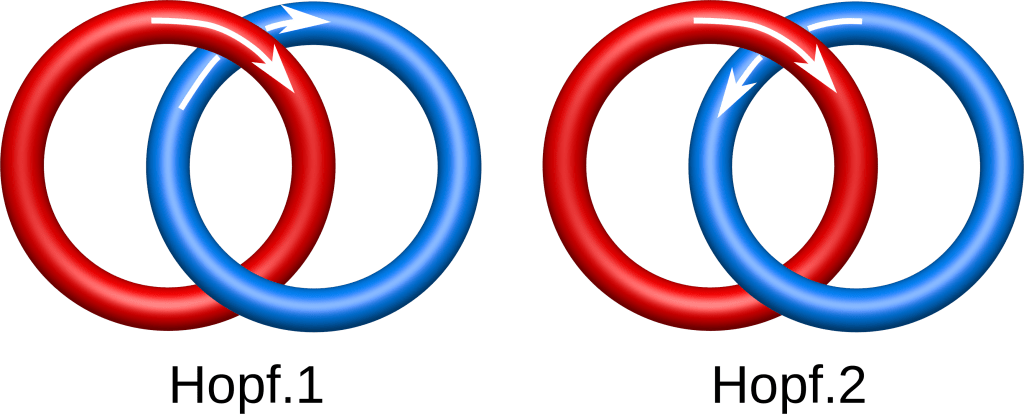
Nella teoria dei nodi, l’intreccio di Hopf rappresenta il più semplice esempio di intreccio non banale e non connesso, cioè formato da più componenti. Il suo Gln è pari a ±1, a seconda dell’orientazione scelta, e non è omotopicamente equivalente all’unlink — la configurazione di due cerchi disgiunti e separabili. Per capirci: due oggetti (o funzioni, o curve) sono omotopicamente equivalenti se si possono trasformare l’uno nell’altro senza strappi né incollature, solo attraverso una deformazione continua. Pensate a una ciambella e a una tazza con manico: anche se sembrano diversi, in topologia sono omotopicamente equivalenti perché si può “modellare” l’uno nell’altro senza tagliare o incollare nulla. Il manico della tazza corrisponde al buco della ciambella.

Il fisico e matematico scozzese Peter Guthrie Tait era un accanito fumatore di pipa ed era talmente affascinato dagli anelli di fumo che costruì un paio di apparecchi per crearli. Era così entusiasta del suo lavoro che lo mostrò a William Thomson, Lord Kelvin. Osservando gli anelli velenosi del gas cloro della macchina di Tait eseguire le loro acrobazie, Thomson concluse che gli elementi chimici dovevano essere in realtà vortici annodati di “etere”. Nodi diversi dovevano quindi costituire elementi diversi. Nacque così la teoria atomica dei vortici.


Tait, sempre ammaliato dagli anelli di fumo (a questo punto molti si chiederanno cosa fumasse, e io con loro), venne a conoscenza del lavoro del fisico tedesco Hermann von Helmholtz, il quale aveva dimostrato che i nodi dell’etere — un fluido sottile e privo di attrito, ritenuto all’epoca permeare l’intero universo — sarebbero destinati a persistere indefinitamente. Colpito profondamente da queste teorie, Tait scrisse con entusiasmo: «[i nodi dell’etere] rimarranno per sempre impressi con quel moto vorticoso, almeno fino a quando l’atto creativo che li ha prodotti non li rimuoverà nuovamente». Quando nel 1868 il matematico francese Joseph Bertrand criticò la teoria di Helmholtz, su suggerimento di Thomson Tait contattò l’amico James Clerk Maxwell, fisico e matematico scozzese a sua volta incuriosito dagli sviluppi della teoria atomica dei vortici per l’analogia tra il flusso dei fluidi e l’elettromagnetismo. La teoria dei vortici e gli anelli di fumo spinsero Tait a studiare i nodi e, nel 1877, egli pubblicò On Knots (Sui nodi), il primo lavoro matematico con la parola ‘nodo’ nel titolo.

Tait non era consapevole del lavoro del matematico tedesco Johann Benedict Listing, allievo di Gauss, dal titolo Vorstudien zur Topologie (Studi preliminari sulla topologia, 1847), dove introdusse il termine topologia. «Per topologia intendiamo lo studio delle relazioni modali delle immagini spaziali, ovvero delle leggi di connessione, disposizione reciproca e tracce di punti, linee, superfici, corpi e loro parti o loro unioni nello spazio, indipendentemente dalle relazioni di misure e quantità» (Listing 1847). Una successiva opera di Listing, Der Census räumlicher Complexe (Il censimento dei complessi spaziali) conteneva i primi passi nella direzione della teoria dell’omologia, che Maxwell abbracciò nel suo Treatise on Electricity and Magnetism (Trattato sull’elettricità e il magnetismo, 1873).
Maxwell informò Tait dell’opera di Listing e Tait gli chiese un parere peer-to-peer sulla sua opera On Knots. In particolare Tait era angustiato dagli anelli di Borromeo (o Nodo Borromeo): «Come possiamo definire la “connessione” della disposizione [Figura 1], in cui non vi è alcun collegamento ma non è possibile separare gli anelli? Se si modifica un qualsiasi segno [incrocio], un anello si stacca, ma viene introdotto un grado di connessione! Non si tratta né di un nodo né di un collegamento. Che cos’è?».


Non sappiamo i commenti di Maxwell alla teoria dei nodi dell’amico, ma in compenso gli inviò il seguente poema.
(Cats) Cradle Song,
By a Babe in Knots.
PETER the Repeater,
Platted round a platter
Slips of slivered paper,
Basting them with batter.
Flype ’em, slit ’em, twist ’em,
Lop-looped laps of paper;
Setting out the system
By the bones of Neper.
Clear your coil of kinkings
Into perfect plaiting,
Locking loops and linkings
Interpenetrating.
Why should a man benighted,
Beduped, befooled, besotted,
Call knotful knittings plighted,
Not knotty but beknotted?
It’s monstrous, horrid, shocking,
Beyond the power of thinking,
Not to know, interlocking
Is no mere form of linking.
But little Jacky Horner
Will teach you what is proper,
So pitch him, in his corner,
Your silver and your copper.
(Ninnananna dei Gatti)
Di un Bimbo tra i Nodi
Pietro il Ripetente,
intreccia su un piattino
strisce di carta argentea,
le impasta con farina.
Rigira, taglia, torce,
anelli di carta annodata;
traccia il suo sistema
sulle ossa di Nepero.
Slega il groviglio storto
in trama ben tessuta,
blocca nodi e incastri
in rete interconnessa.
Perché mai un uomo cieco,
ingannato, raggirato,
chiami nodi promesse,
non nodosi ma annodati?
È mostruoso, assurdo, orrendo,
oltre ogni pensiero umano,
non sapere che l’intreccio
non è solo un semplice legame.
Ma il piccolo Gianni Angolino
ti insegnerà il giusto modo:
lanciali nel suo cantuccio,
i tuoi spiccioli d’argento e rame.

È interessante il riferimento di Maxwell al gioco del Ripiglino che secondo gli etnologi era giunto in Gran Bretagna solo nel XVIII secolo, portatovi dai marinai della compagnia delle Indie Orientali. Il Ripiglino è citato nella novella popolare The Last Chronicle of Barset di Anthony Trollope, uscita nel 1867 e che probabilmente Maxwell aveva letto. Nella poesia vi sono alcuni riferimenti specifici tipo: Bones of Neper si riferisce ai bastoncini di Nepero, strumenti di calcolo, chiaro riferimento all’accenno di Tait di aver ideato un sistema per risparmiare tempo utilizzando pezzi di cartone «in qualche modo simili» alla Radbologia di John Napier. Flype ’em è un termine tecnico nei nodi e nella teoria dei link, mentre beknotted è un neologismo introdotto da Tait per riferirsi alla “nodità” ovvero quello che oggi nella teoria dei nodi si chiama “numero di incroci”. “Jacky Horner” è personaggio di una nursery rhyme (filastrocca) inglese nome che ho tradotto con “Gianni Angolino” per conservare il diminutivo e il riferimento spaziale, tuttavia all’epoca, la maggior parte dei matematici che sentivano il nome “Horner” avrebbe immediatamente pensato al metodo di Horner in algebra.
(Continua)
***
Articolo di Flavia Busatta

Laurea in Chimica. Tra le fondatrici di Lotta femminista (1971), partecipa alla Second World Conference to Combat Racism and Racial Discrimination (UN Ginevra 1983) e alla International NGO Conference for Action to Combat Racism and Racial Discrimination in the Second UN Decade, (UN Ginevra 1988). Collabora alla mostra Da Montezuma a Massimiliano. Autrice di vari saggi, edita HAKO, Antrocom J.of A.


